
|
|
|
カテゴリ:算数
解法編です。
中学受験向けだとこんなエレガントな解法があります。 おしゃれな解法 こんなおしゃれな解法はできませんでした。どろどろです。 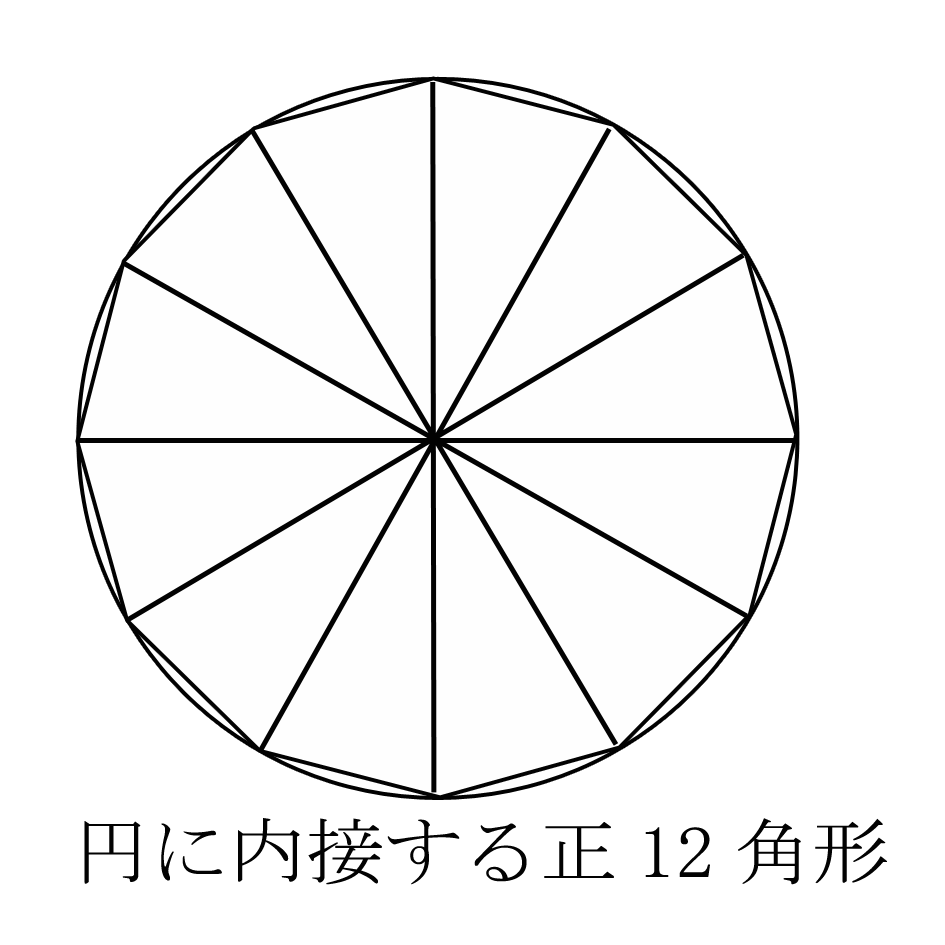 半径1の円に内接する正12角形を考えました。 この円の円周は2πです。 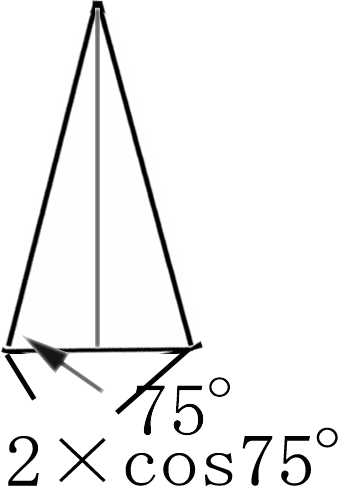 従って加法定理より、 cos75度=cos30度cos45度-sin30度sin45度 =√3/2×√2/2-1/2×√2/2 内接する正12角形の外周の長さは 12×2×(√3/2×√2/2-1/2×√2/2) =6×(√6-√2) ここで近似値を求めると ≒6×(2.449-1.414) ≒2×3.10・・・ 円に内接する多角形の外周の長さはその円よりも小さいので π>3.10・・・ 従ってπは3.05よりも大きい。 内接する正六角形を考えたら、円周率は3よりも大きいことは求められます。同様に外接する正六角形を考えると 2/√3×6=4√3≒2×3.46・・・ なので、3.5よりも小さいことが証明できます。 外接する正多角形の辺の数を増やせば、精度は上がります。 中学生向けにはcos75度の値を教えておいて平方根の計算に持ち込むのもありかと。 或いは相似から辺の長さの比を出すのもありですね。 最初にお伝えしたサイトにはもっとエレガントな解法があります。 まあ、数学苦手な人間が考えるとこんなもの、ということで。 お気に入りの記事を「いいね!」で応援しよう
[算数] カテゴリの最新記事
|
|