
|
|
|
カテゴリ:よもやま話
☆ 9月21日(火曜日) 旧八月十四日 甲戌 先負: 秋の交通安全運動
前回のブログにちょっと補足しておいたほうが良さそう(より楽しんでいただけそう)なので、追加しておくことにしよう。 【フィボナッチ数列】 フィボナッチ数は13世紀に、かのレオナルド・ダヴィンチが気付いた数列だそうだ。彼の顕わした「算盤の書」という本がある。これは当時の会計士向けの教科書だったそうで、この中に練習問題として出てくる。 『一人の男が壁で囲まれた閉じた部屋の中に一つがいのウサギを入れた。このウサギ夫婦は毎月新たに一つがいのウサギを産む。生まれたウサギのつがいは、次の月になると、又新たにつがいを一組ずつ産み始める(生まれた月には子ウサギは産まない)。こうしてウサギが増えていくとすると、一年後にウサギは何匹になっているだろうか。』 これがダヴィンチの問題である。 これをウサギのつがいの数で表すと、1、2、3、5、8、13、21、34、・・・となる。これを1年後まで辿ると答えが出てくるのだ。(答えは377*2) フィボナッチ数列は今では0から開始するようになっており、0、1、1、2、3、5、8、13、21・・・と表すのが普通だ。つまりフィボナッチ数とは、「直前の二項の数の和を現在の項の数とする」という規則で出来上がる数列のことだ。 この数列はダン・ブラウンの小説(映画にもなった)「ダ・ヴィンチ・コード」の中にも出てきたので、ご存知の方も多いだろう。因みにダヴィンチはこの功績(?)で、やがて「レオナルド・フィボナッチ」というあだ名で呼ばれるようにまでなってしまった。ダヴィンチの本名は「レオナルド・ピサーノ・ビゴッロ」である。 このフィボナッチ数列、実は自然にも色々な場所で出て来る。 例えばパイナップルの甲羅(?)模様の配列、ひまわりの花の花芯の模様、巻貝の縦断面のカーブなどは、フィボナッチ数列に従っている。この辺は前のブログで紹介したYouTubeの動画でご覧になることが出来る。 いくら万能の天才ダビンチでも、花や貝にフィボナッチ数列を教えることは出来ない。又、花や貝がフィボナッチ数列を知っているはずも無い。これらは自然に形成された不思議である。 上にはウサギの例を引いたが、これは少し人為的で不自然である。一つがいのウサギの夫婦からいつでも雄雌一匹ずつのウサギが都合よく生まれるわけはない。 そこでフィボナッチ数列を読み替えて、 『最初は木の幹から一本の枝が芽を出す。ある時間が経過すると2本に枝分かれする。それぞれの枝は又ある時間が経過すると2本に枝分かれする。・・・・』と解釈すると、自然には「自然に」ありそうな状況である。 これを更に、「貝の細胞が、自らも分裂しながら貝殻の成分を分泌する量」、或いは「ひまわりの花の中で花が形成されていく過程」などと読み替えれば、フィボナッチ数列が自然界で多く観られることも納得できそうである。 この辺が上記の動画にはうまく表現されていて美しい。因みに「黄金比」もこのフィボナッチ数列と関連付けて説明できる。 ダビンチの頭と自然とはここで結びつくのである。 【パズル問題再録】 やはり前回のブログでパズルの問題を掲載した。 『ついでだからお慰みにパズルを一つプレゼント。古典的なパズルだから多くの人がご存知だろう。 「川岸にワニとウサギとニンジンの束がある。農夫はこれらを船で向こう岸に運ばなければならない。船には、一度に農夫の他にはワニかウサギかニンジンの束の何れか一つしか載せられない。」 これが問題。 勿論ワニとウサギを一緒にして、農夫が居ないままにしておけば、ウサギはワニに食べられてしまう。ニンジンもウサギの大好物だ。 この問題を、ここに掲げた立方体のカゴのイメージを利用して、「スマートに」解いて欲しい。』 という内容だった。 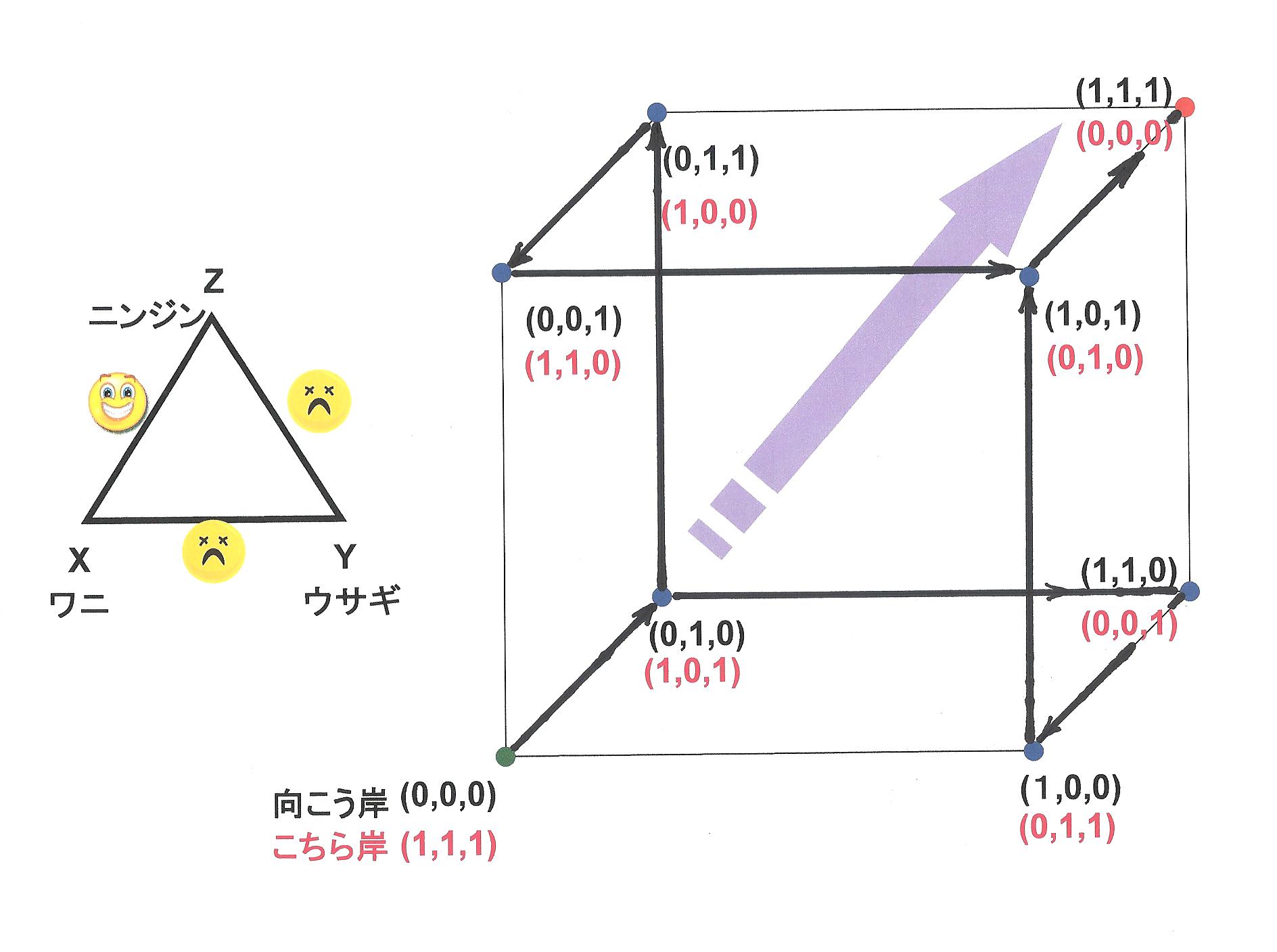 ところが参考に掲げた図が随分見辛いものだったので、何のことか分からない方も多かったろうと拝察する。ここで、その図を再び掲げてみる。今度は見やすくなっただろうと思うのだが・・・ ところが参考に掲げた図が随分見辛いものだったので、何のことか分からない方も多かったろうと拝察する。ここで、その図を再び掲げてみる。今度は見やすくなっただろうと思うのだが・・・この問題はワニやウサギを「オオカミ、ヤギ、キャベツ」に入れ替えるなどしてみることが出来る。要するに、「三すくみ」ではなく「二すくみ」の関係にあるものなら何でもよい。本質は「A,B,C三者の作る立方体空間を考えて、一方の頂点から反対側の頂点にまでたどり着くにはどうしたらよいか?」という問題に帰着するのだ。こうして特殊な問題を一般化することは、学者先生たちが様々な分野で普段行っていることでもあるのだ。 お気に入りの記事を「いいね!」で応援しよう
最終更新日
2010.09.22 15:32:25
コメント(0) | コメントを書く
[よもやま話] カテゴリの最新記事
|