2021年から正月の定番になった数学パズル。
主に虫食い算と覆面算にチャレンジしている。
今回は、
虫食い算の
掛け算に挑む。
虫食い算とは、計算に空いた穴を埋める数学パズルだ。
筆算の式と、すでに判明している数字を手掛かりに、空欄を埋めていく。
同じ数字を何度使ってもよい。
問題引用元:
https://twitter.com/tb_lb/status/1741784463724671046
では、解くとしよう。
かけられる数をAB2、かける数をC2D、さらに各段階の計算を①~④とおく。
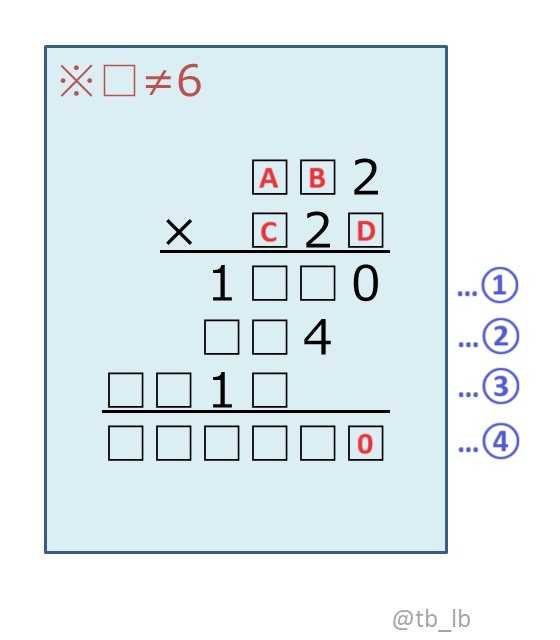
まず、計算①「AB2×D=1□□0」を見る。
積の1の位が0となるDは0か5だが、明らかにD=0ではないので
D=5。
計算①は「AB2×5=1□□0」となる。
積の1000の位が1なので、1000≦AB2×5<2000、さらに200≦AB2<400が成り立つ。
よって、Aは2か3に絞られる。
さらに、Bが奇数だと積の10の位が6になる。これは条件の□≠6に反する。
B=6も無いため、残るBの候補は0,2,4,8となる。
ここで計算②「AB2×2=□□4」を見る。
B=3とB=8は、積の10の位が6となるため除外。
よって残るBは0,2,4だが、いずれの場合でもA=3が入ると「3B2×2=6□4」で条件に反する。
以上よりA=3は解なしとなるため、
A=2が確定する。
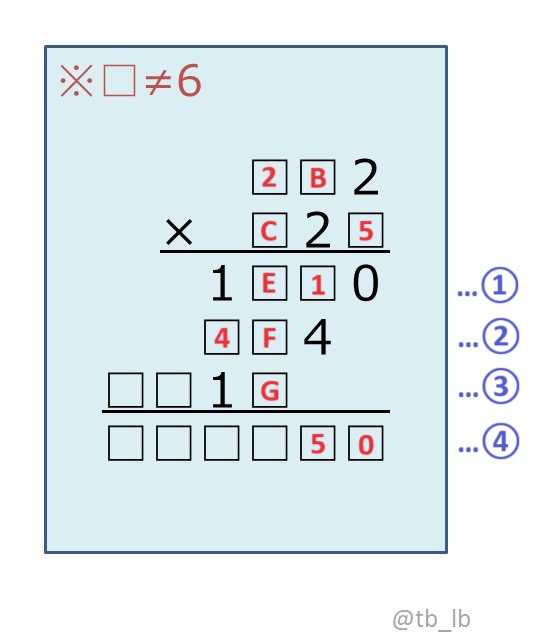
現状では計算④の1000の位が6になるため、100の位で繰り上がりが求められる。
該当する□を、計算①より順にE,F,Gとおく。
B=0ではE=0、F=0となり、Gにかかわらず繰り上がらない。よってB≠0。
B=2ならばE=1、F=4で、G≧5なら繰り上がる。
ところが、計算③「222×C=□□1G」の10の位が1となるのはC=5のみで、この場合G=0となる。よってB≠2。
消去法で
B=4となる。
この時、E=2、F=8で繰り上がりの条件も満たす。
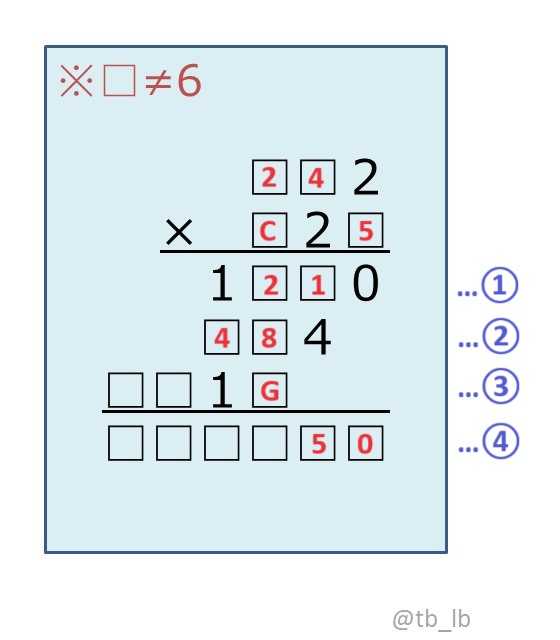
最後に、もう一度計算③「242×C=□□1G」を見る。
10の位が1となるのは、
C=5の場合のみ。
以下の通り残りの空欄に6が入らず、計算を完成させることができる。
従って、この計算の正体は
「242×525=127,050」である。
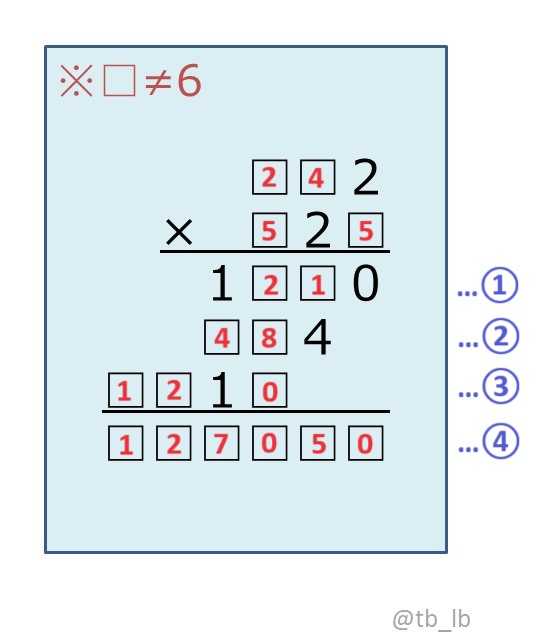
解けたはいいが、力技に頼ってしまった感がある。
もっとスマートに解きたいものだ。
First updated 2024.01.12 08:18:24
