2021年から正月の定番になった数学パズル。
もう1問、
虫食い算の割り算に挑戦しよう。
問題引用元:
https://twitter.com/tb_lb/status/1742147584268050655
割る数をAB2、商をCDEF、4段階の計算を順に①~④とおく。
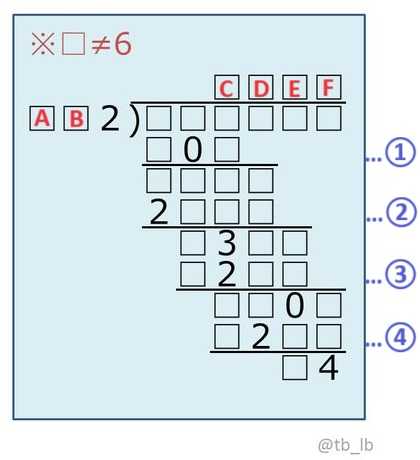
計算②「AB2×D=2□□□」より、「AB2×D≧2000」となるA,B,Dの組が存在する。
D=9だとしてもAB2≧222.22…となるため、1の位が2であることも考慮し割る数は232以上である。
さらに計算①「AB2×C=□0□」より「AB2×C<1000」なので、割る数が232以上ならC≦4。
C=4ならば「AB2×4=□08」。
計算①の積が3桁となる割る数は232と242しかないが、いずれも積の10の位が0とならないので不可。
C=3ならば「AB2×3=□06」で□≠6の条件に反する。
C=2ならば「AB2×2=□04」となり、積の10の位が0となるBは0と5のみ。
さらに前述より割る数は232以上、「AB2×2<1000」より500未満。
以上を満たす割る数の候補は、252、302、352、402、452が挙げられる。
しかし「302×2=604」で□≠6に反するため、302は除外される。
この条件を計算③「AB2×E=□2□□」に適用する。
4つの割る数候補で、積の100の位が2となる計算は以下の通り。
252×5=1260
402×3=1206
402×8=3216
452×5=2260
いずれも□≠6に反するので不可。
C=2は解なし、よって
C=1が確定する。
この時計算①「AB2×1=□02」を満たすのは
B=0のみ。
割る数の条件よりA≧3も確定。
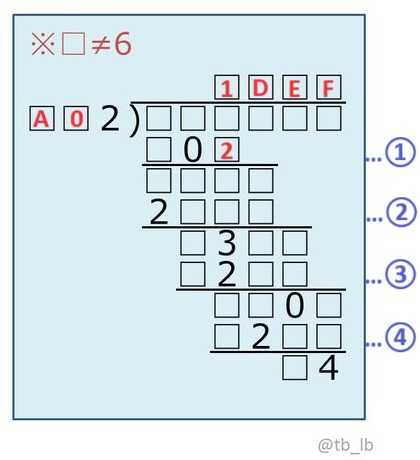
計算②「□□□□-2□□□=□3□」、4桁から4桁を引いて3桁になるので
引かれる数の1000の位は3か2、よってA≦7。
残るAより、割る数の候補は302, 402, 502, 702。
この候補を再び③「AB2×E=□2□□」に適用する。
積の100の位が2となる計算は以下の4つ。
302×4=1208
402×3=1206
402×8=3216
702×6=4212
このうち、□≠6に反しない計算は1つ目のみ。
A=3、E=4、F=4が確定する。
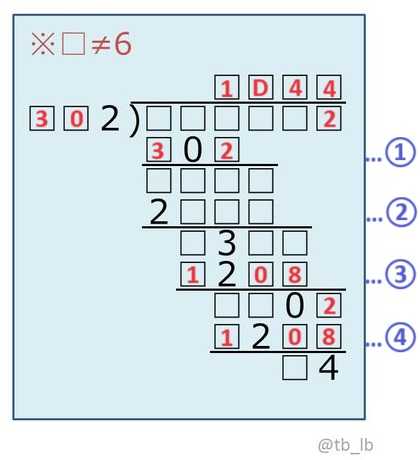
計算②「302×D=2□□□」より「302×D≧2000」、これを満たすのはD≧7。
ただしD=8ならば「302×8=2416」で不可。
D=7、つまり商が1744ならば「302×1744=526,688」だが
余り「□4」を加えても割られる数の1000の位を6から変えることができない。よってD≠7。
D=9で商が1944ならば「302×1944=587,088」で成立する。よって
D=9。
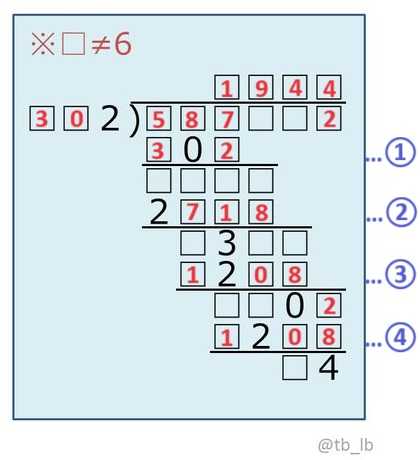
最後に、余りを求める。
余りの1の位はすでに4が入っているため、割られる数の1の位は2。
計算④「□□02-1208=□4」、これを満たすのは「1302-1208=94」しかない。
余りは94。
以下の通り残りの空欄に6が入らず、計算を完成させることができる。
従って、この計算の正体は
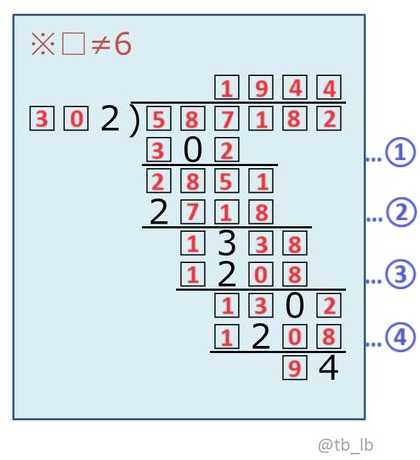
「587182÷302=1944余り94」である。
解けたはいいが、
なんと美しくない。
こんな解き方しかできない自分が情けなくなるね本当にorz
掛け算も含めて、今年はこれまで以上に難しかった。
2024と6という、
手掛かりになる数字が偶数ばかりなので
あり得る可能性を絞り込むのが困難になる。
実は他に覆面足し算をひとつ見つけたのだが、あまりにも難しい。
僕としたことが、降参を余儀なくされた。
繰り上がりのために場合分けがやりづらい足し算の覆面算や虫食い算は、思った以上に難問になることがある。
総じて、例年よりも苦戦続きの正月数学パズルだった。
First updated 2024.01.23 08:12:18
