
|
|
|
カテゴリ:音楽
この週末、とある音楽関係のブログを眺めていたところ、「協和音の条件は、組み合わせられる音(の波長、あるいは振動数)が互いに整数比の関係になっていること」というこれまでの常識が覆された、という最近の研究成果なるものが話題になっていました。
研究者が所属するケンブリッジ大学のサイトにある紹介記事をDeepL訳を基に引用すると以下のようになります。 ピタゴラスは間違っていた:普遍的な音楽のハーモニーは存在しないとの研究結果要約すると、 (1)ヒトが「協和音」と感じる音同士の関係は、ピタゴラスが言うような完全な整数比になっていない。 (2)「協和音」は、音律だけでなくそれを奏でる楽器の音色にも強く依存し、普遍性を持たない。 となるかと思われます。(ちなみに、1は中学校の数学で習う「ピタゴラスの定理」とは無関係です。) 興味をそそられた亭主、リンク先のネイチャー・コミュニケーション誌のサイトで件の論文を眺めてみました。(ちなみにこの雑誌、有名な自然科学系の雑誌「ネイチャー」の発行元が運営するオンライン出版専門誌で、論文1遍を掲載しようとすると5000ポンド[今の為替レートで〜100万円!]もボッタくられることでも有名。) このような心理学的実験・調査では、そのやり方自体が問題になります。この研究では、西洋音楽で用いられている離散的な音のセット(1オクターブ12音が前提)に縛られないよう、音の振動数が連続的に変えられるような音源ツールが用意され、被験者がそれを変えながら最も調和していると感じる振動数を答えるという仕掛けが用いられました。さらには、楽器によって音色(倍音の振動数や強度の分布)が異なることによる影響も含めて考えるため、独自の音体系を持つ非西洋音楽の楽器が奏でる音の間の協和・不協和も調べてみた、というわけです。(結論は前述の通り。) ここで、まず(1)について亭主がすぐに思い出すのは、西洋音楽の楽器の代表であるピアノですら、通常はヒトの聴覚が持つ「高い振動数ほど低めの音に聞こえる」という特性に合わせて不均等に調律されていることです。これは「オクターブ伸長現象」として調律師の間ではよく知られた事実で、心理的オクターブは物理的オクターブよりも最大で数十セント広がるので、チューナーなどで機械的に倍音に合わせると不快感をもたらすとのこと。 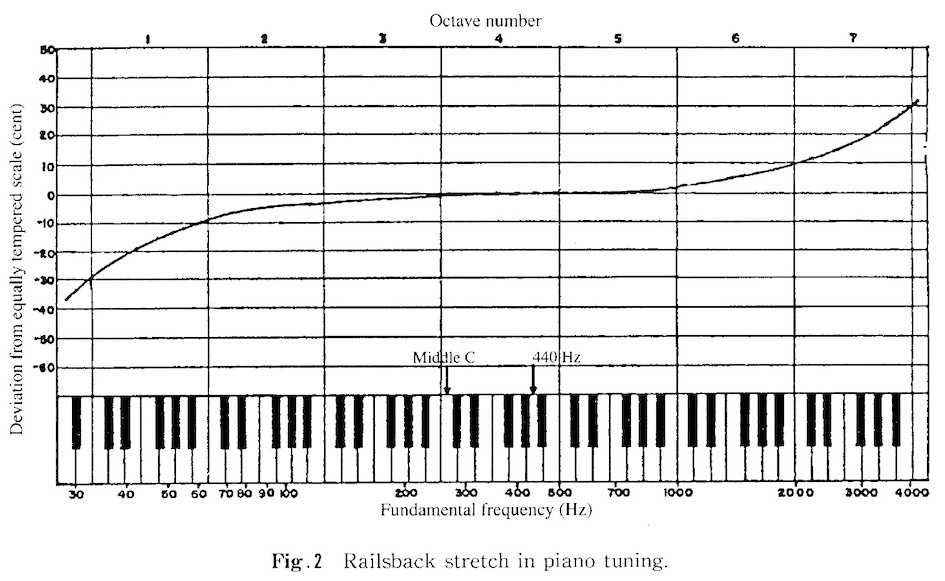 さらに、実際の楽器が奏でる音は数多の倍音を含むことを考えると、2つの音の協和・不協和が倍音同士の関係からも少なからず影響を受けることが容易に想像されます。実際、上記の研究では倍音列の振動数間隔を少し引き伸ばした場合と圧縮した場合とで協和と感じる度合いを調べ、両者が大きく異なる音同士で協和・不協和を感じさせることが示されています。 というわけで、ピタゴラスが考えた「整数比(数学)がヒトの感覚(協和音)を支配する」という公理は文字通り思弁による絵空事でしかなく、現実の音楽が関わる人間の耳、楽器の音のいずれもこのようなルールには従わない、という事実が改めて確認されることになりました。まぁ、言われてみれば当たり前のようにも感じますが、我々は普段、ピタゴラス流の「偏見」からどれほど自由だっただろうか、と反省させられるところでもあります。 なお、心理的オクターブが広がるメカニズムについては必ずしも研究者の間でコンセンサスは得られていないようですが、有力な説としては、ヒトの聴覚神経上で伝わるパルスの頻度は音の高さに比例するものの、パルス頻度が増大ると神経系の応答が追いつかなくなり始める(つまりパルス頻度が音高に比例しなくなる)ことによるとのこと。(この辺については大串健吾さんという方の解説記事(日本音響学会誌 59巻3号)に詳しいので、ご興味のある方は参照されたし。上の図もこれからの引用。) 「何世紀にもわたる西洋音楽理論を覆す」というこの音響心理学的研究、クラシック音楽が暗黙理に前提としてきた音楽的先入観を打破するという意味でインパクトがあります。ビートルズが好んでカバーしたチャック・ベリーの曲を真似していえば「Roll Over Pythagoras(ピタゴラスなんかぶっ飛ばせ)」といったところでしょうか。  お気に入りの記事を「いいね!」で応援しよう
Last updated
March 3, 2024 10:47:03 PM
コメント(0) | コメントを書く
[音楽] カテゴリの最新記事
|